Bayesian bi-clustering of categorical data

Alberto Pessia

_{^{Department of Mathematics and Statistics, University of Helsinki}}

European Meeting of Statisticians
Helsinki, 24-28 July 2017

Motivation: identify groups of homogeneous proteins

Clusters naturally arise as a consequence of evolutionary processes

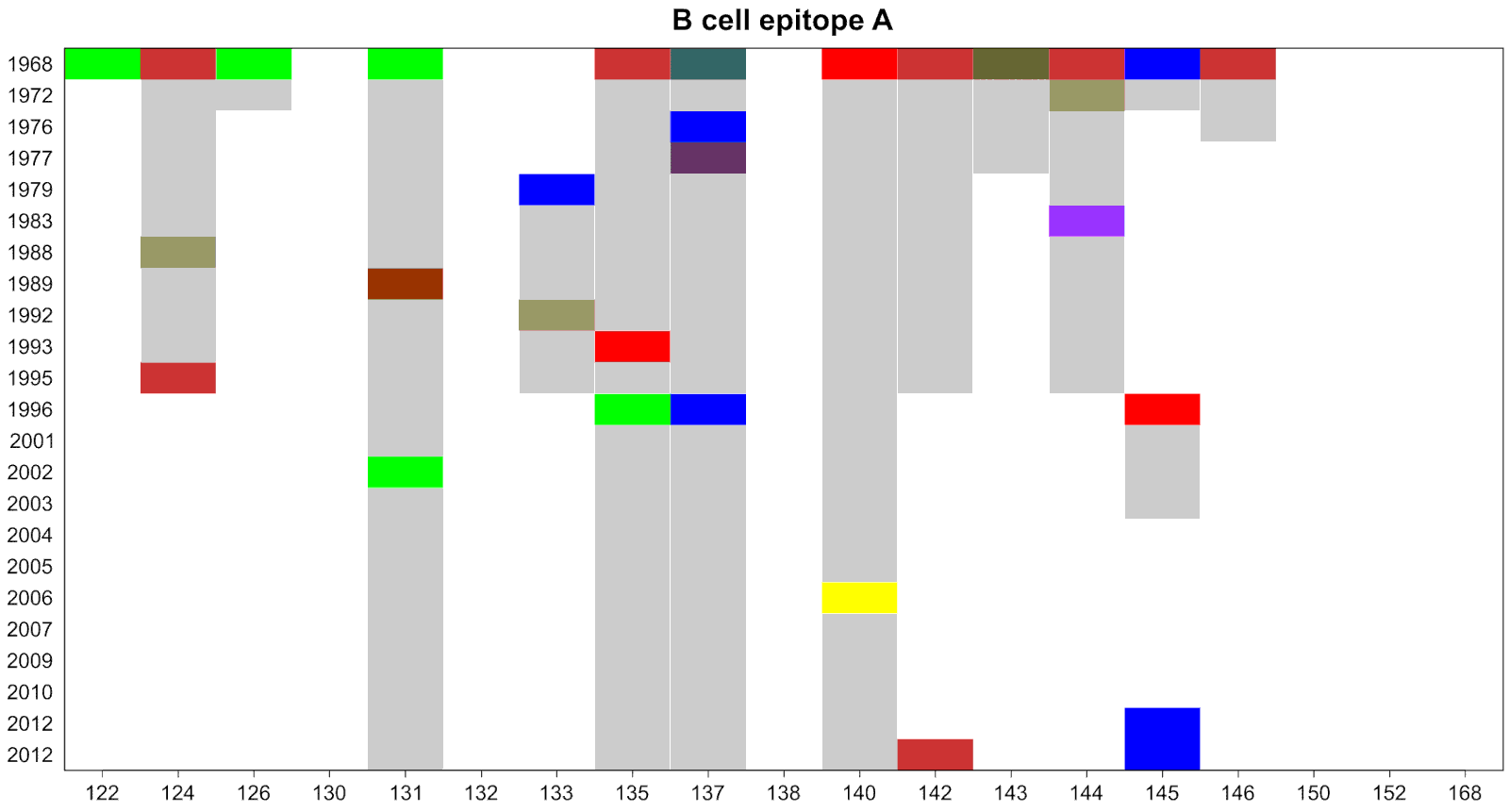
Motivation: identify important amino acids

Classify the sites and their corresponding amino acids according to their discriminatory power

Categorical data

• No expected value, median, variance, etc.

• Operations are done on counts and their probabilities

High dimensional

• Usually thousands of rows and columns in the data matrix

• Number of columns much greater than the number of rows

Bi-clustering

• Partition the rows into blocks

• Partition the columns into blocks as well

Bayesian analysis

• Informative priors to regularize the likelihood

• Posterior distribution to measure our uncertainty

Computation

• Stochastic optimization to find the MAP

• MCMC algorithms to explore the posterior

• High costs for large dataset

Cluster analysis of categorical data

Status: Noise

We just received a black ball. In which cluster would you put it?

Status: Weak signal

We just received a black ball. In which cluster would you put it?

Status: Strong signal

We just received a black ball. In which cluster would you put it?

Partitioned data matrix

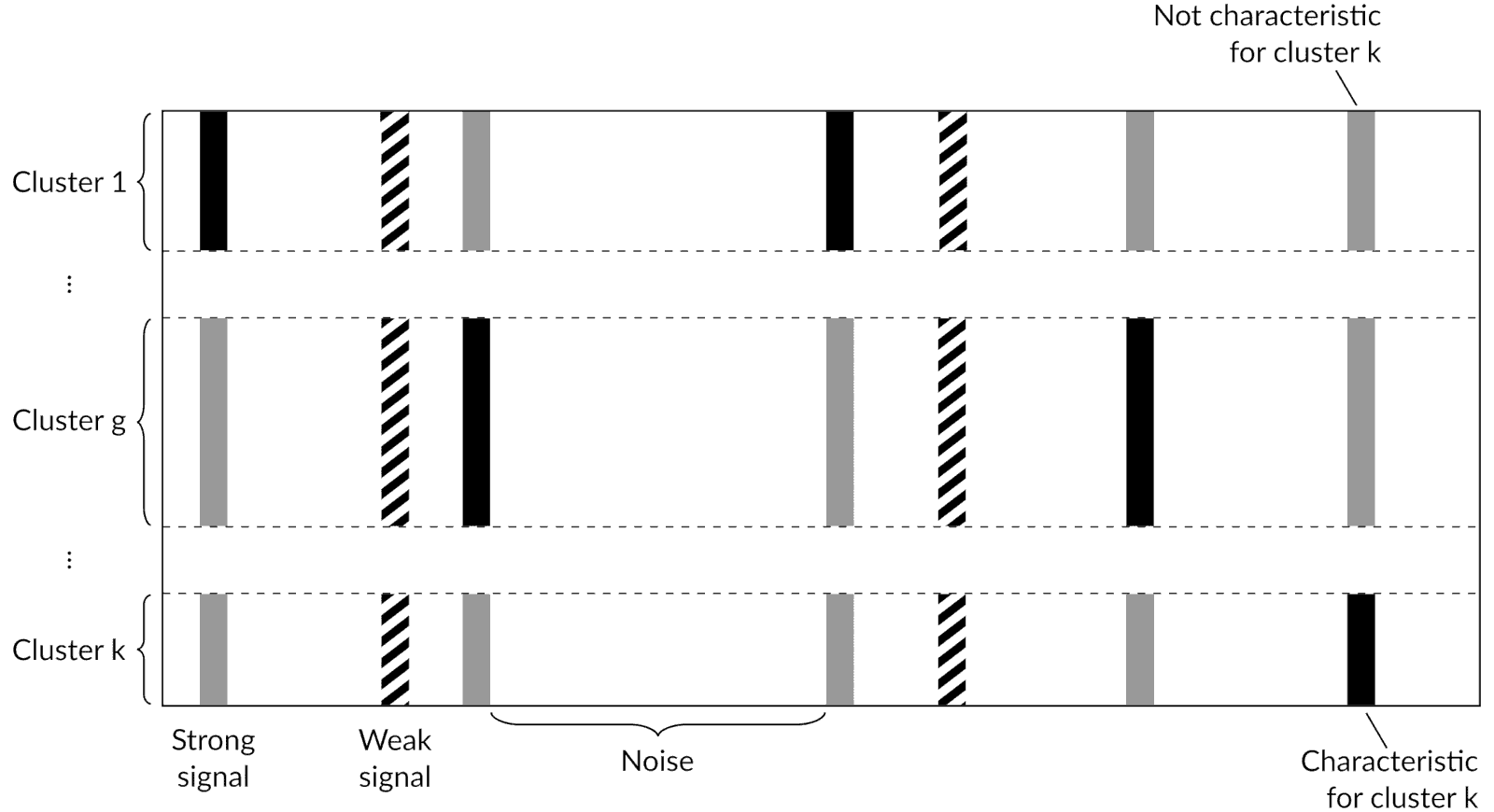
Model parameters

$k$ = total number of clusters

$R_{k}$ = partition of the rows into $k$ clusters

$C_{k}$ = partition of the columns among the $k$ clusters

where

$$ R_{kit} = \begin{cases} 1 & \text{if }i\text{ and }t\text{ belong to the same cluster}\\
0 & \text{otherwise} \end{cases} $$

$$ C_{kjgl}^{u} = \begin{cases} 1 & \text{if }j\text{ has status }u\text{ and property }l\text{ in cluster }g\\
0 & \text{otherwise} \end{cases} $$

Prior distribution on $R$

Model is flexible enough to accommodate any prior distribution on $(k, R_{k})$

In our implementation we used the Ewens-Pitman distribution

$$p(k, R_{k}) = \frac{\Gamma(\psi)}{\Gamma(\psi + n)} \frac{\Gamma(\psi / \phi + k)}{\Gamma(\psi / \phi)} \phi^{k} \cdot$$

$$\cdot \prod_{g = 1}^{k} \frac{\Gamma(n_{g} - \phi)}{\Gamma(1 - \phi)}$$

Prior distribution on $C_{k}$

Independently classify each column $j$ with probabilities $\gamma_{j} = (\gamma_{j1}, \ldots, \gamma_{ju}, \ldots, \gamma_{jv})^{\prime}$

If $j$ is classified as $u$, independently sample within cluster $g$ with probabilities $\omega_{jg}^{u} = (\omega_{jg1}^{u}, \ldots, \omega_{jgl}^{u}, \ldots, \omega_{jgs_{u}}^{u})^{\prime}$

Joint distribution is then

$$p(C_{k} | k) = \prod_{j = 1}^{m} \prod_{g = 1}^{k} \prod_{u = 1}^{v} \prod_{l = 1}^{s_{u}} \left(\gamma_{ju}^{\frac{1}{k}} \omega_{jgl}^{u}\right)^{c_{jgl}^{u}}$$

Bayesian bi-clustering model

$$p(k, R_{k}, C_{k} | X) \propto p(k, R_{k}) \prod_{j = 1}^{m} \prod_{g = 1}^{k} \prod_{u = 1}^{v} \prod_{l = 1}^{s_{u}} \left(\gamma_{ju}^{\frac{1}{k}} \omega_{jgl}^{u} p_{jgl}^{u}(x_{gj})\right)^{c_{jgl}^{u}}$$

where $X$ is the categorical data encoded as a presence/absence binary matrix and

$$p_{jgl}^{u}(x_{gj}) = p(x_{gj} | c_{jgl}^{u} = 1) = \int p(\theta | c_{jgl}^{u} = 1) \prod_{i \in g} p(x_{ij} | \theta) d\theta$$

Posterior distribution

We can show that

$$p(X | k, R_{k}) = \prod_{j = 1}^{m} \sum_{u = 1}^{v} \gamma_{ju} \prod_{g = 1}^{k} \sum_{l = 1}^{s_{u}} \omega_{jgl}^{u} p_{jgl}^{u}(x_{gj})$$

$$p(C_{k} | k, R_{k}, X) = \prod_{j = 1}^{m} \prod_{u = 1}^{v} \left(\frac{\gamma_{ju} \prod\limits_{h = 1}^{k} \sum\limits_{t = 1}^{s_{u}} \omega_{jht}^{u} p_{jht}^{u}} {\sum\limits_{a = 1}^{s_{u}} \gamma_{ja} \prod\limits_{h = 1}^{k} \sum\limits_{t = 1}^{s_{u}} \omega_{jht}^{a} p_{jht}^{a}} \right)^{\frac{c_{j..}^{u}}{k}} \prod_{g = 1}^{k} \prod_{l = 1}^{s_{u}} \left[\frac{\omega_{jgl}^{u} p_{jgl}^{u}}{\sum\limits_{t = 1}^{s_{u}} \omega_{jgt}^{u} p_{jgt}^{u}}\right]^{c_{jgl}^{u}}$$

from which we can implement merge-split Metropolis-Hastings and Gibbs sampling algorithms

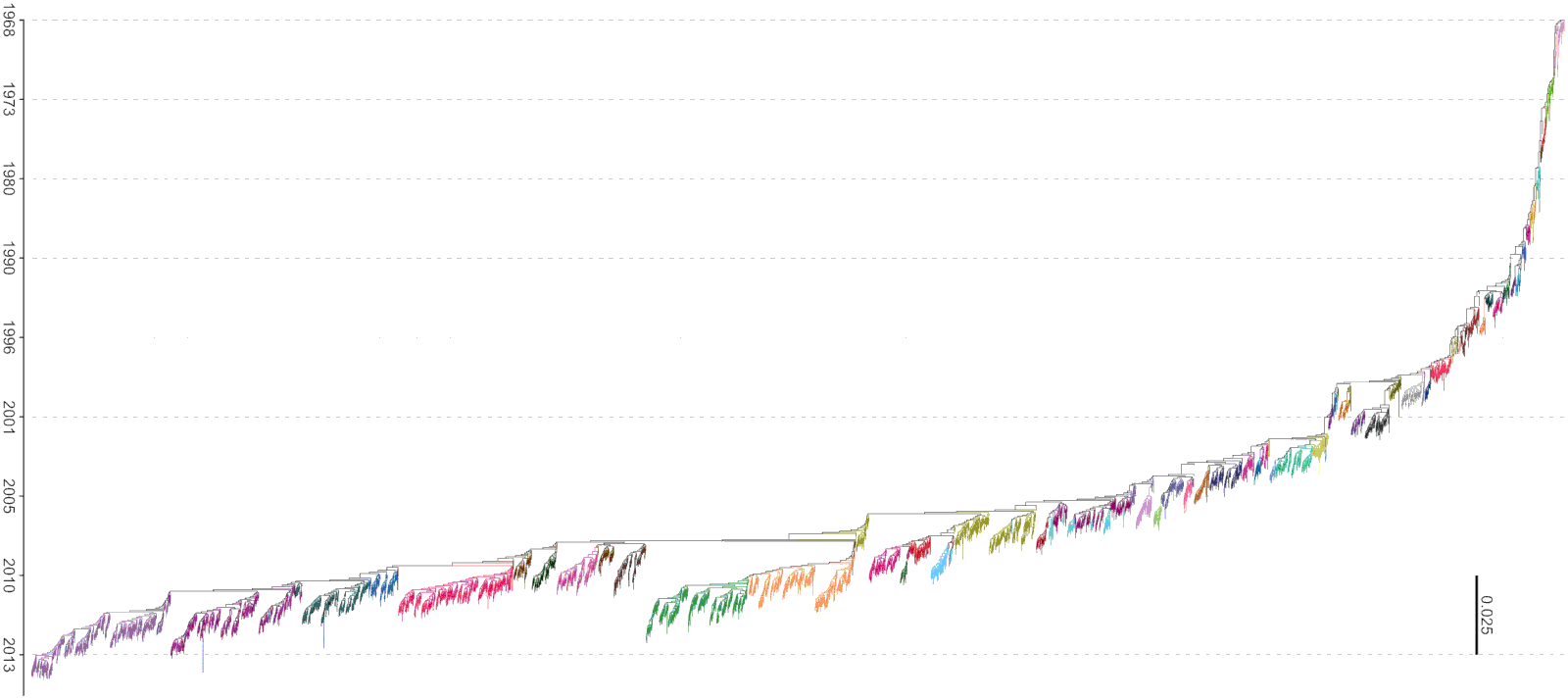
Rotavirus A VP4 protein (clustered data)

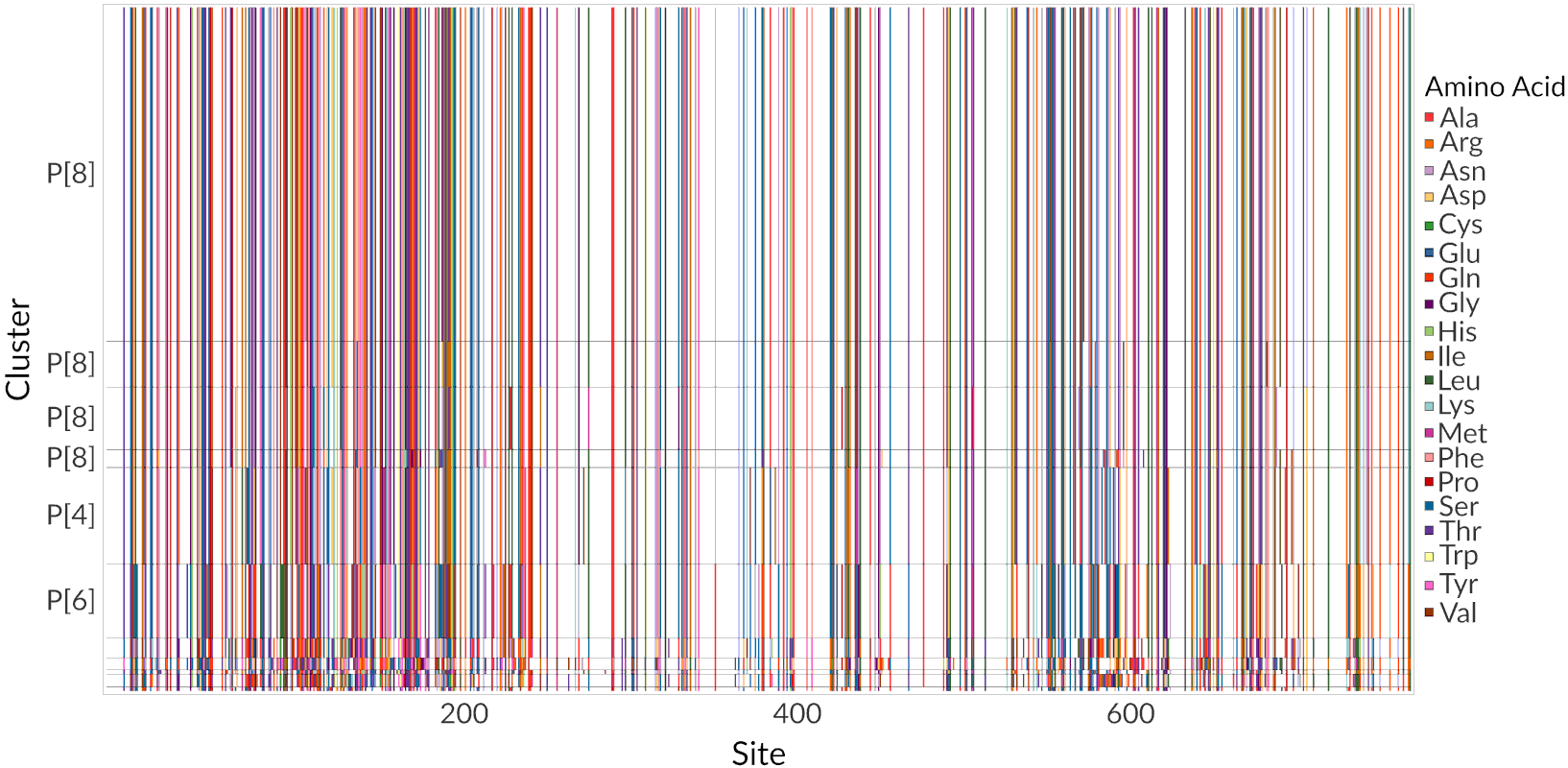
Rotavirus A VP4 protein (Row clusters)

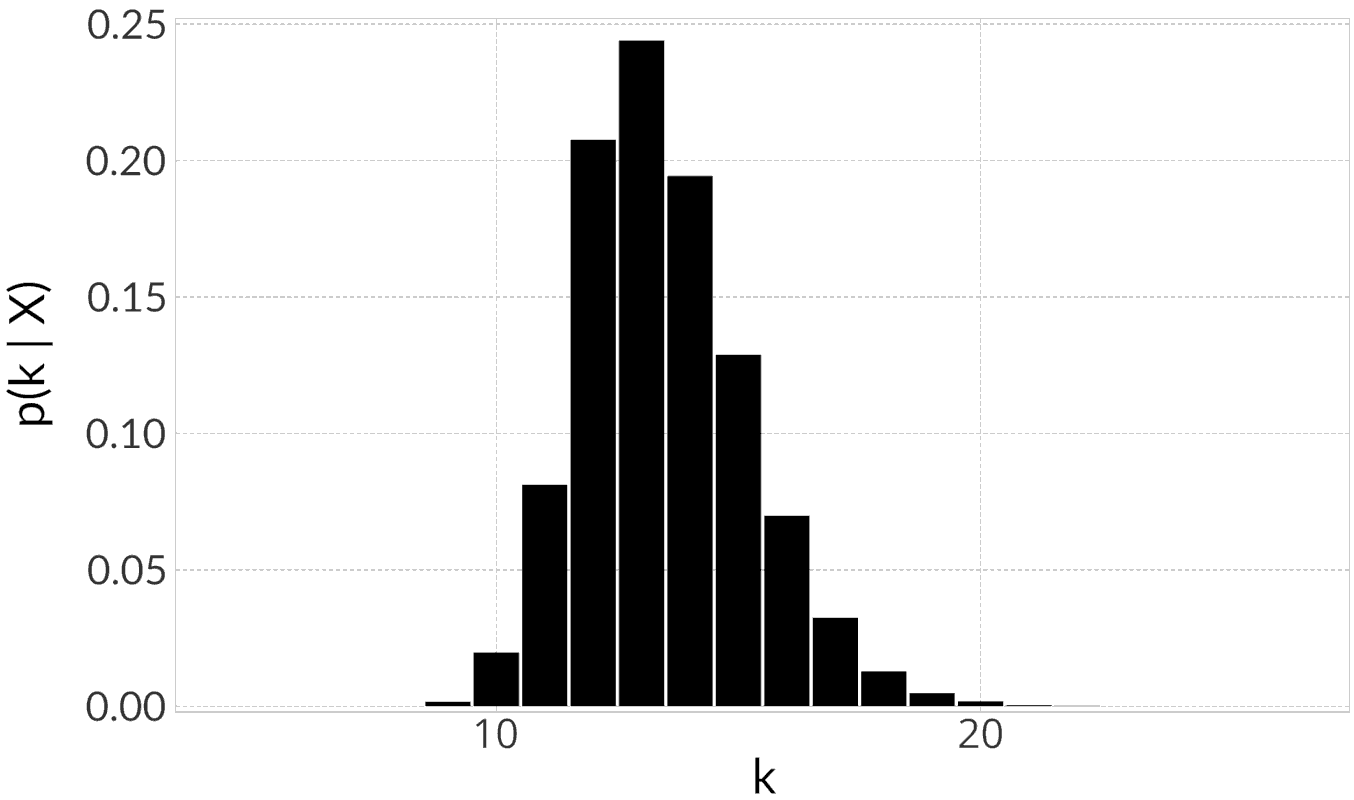
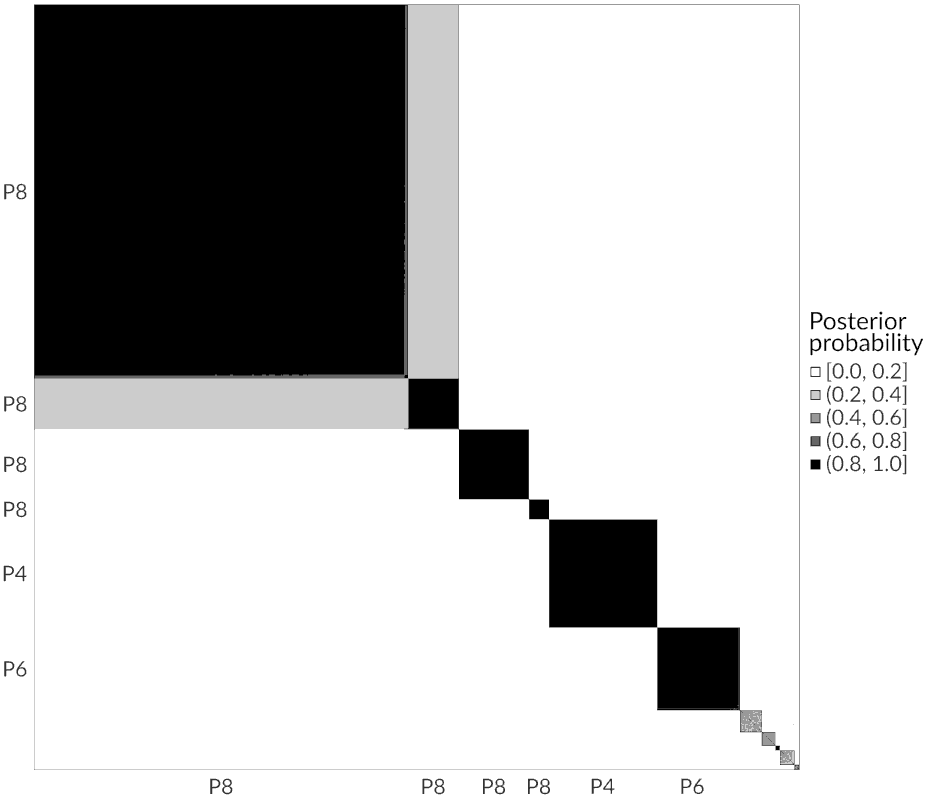
Rotavirus A VP4 protein (Column classification)

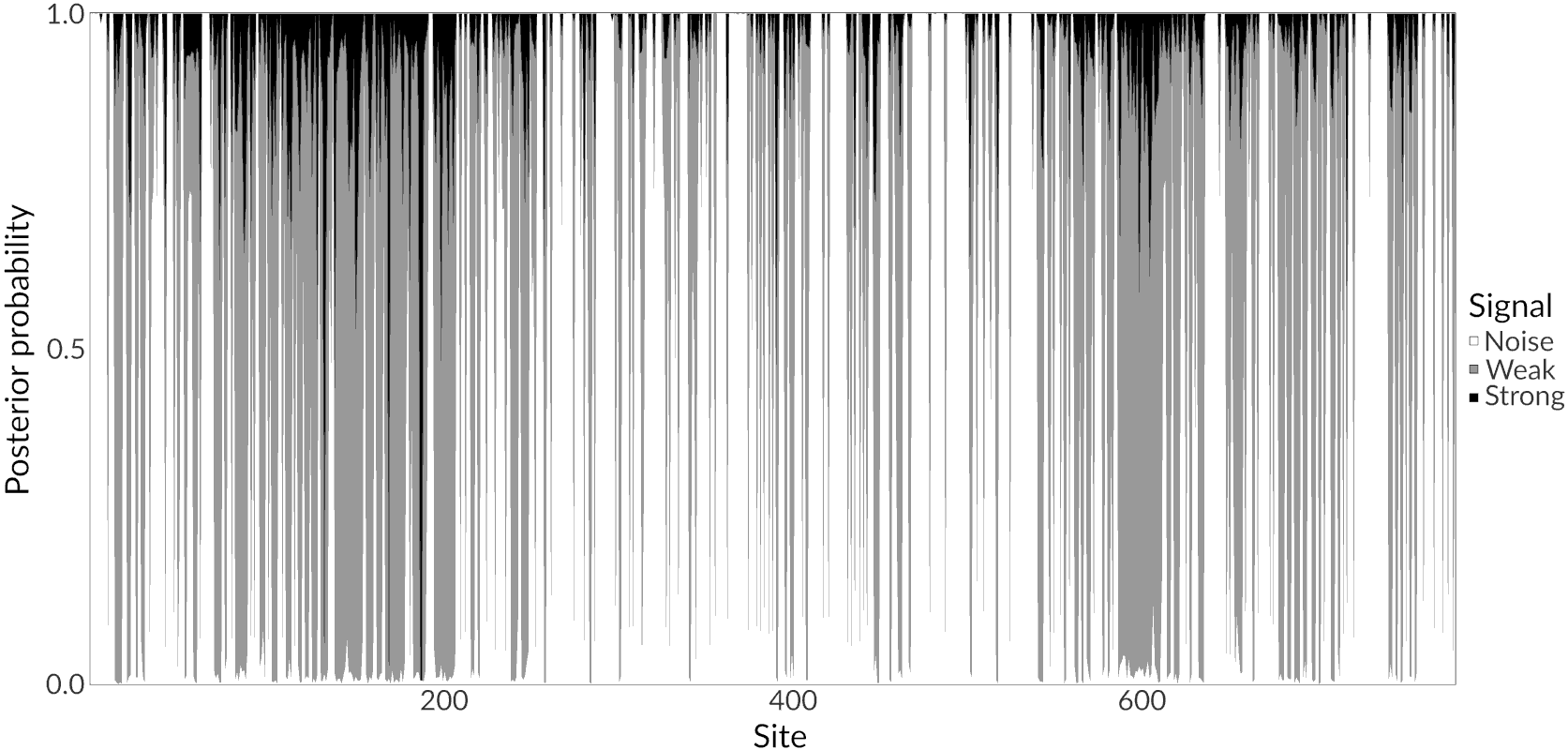
Conclusions

• Model is general enough to be (theoretically) extended to other settings
• Cluster analysis is a computationally hard problem
• MCMC algorithms exist but don’t scale well with the sample size
• Implementation of our model is available as a Julia package: https://github.com/albertopessia/Kpax3.jl